第六节课,课程马上就要过半,还有点小伤感,但是也有坚持到现在到兴奋。这节课换了一个老师,Eric Grimson,MIT的名誉校长,由于下班回来太累,上课太晚没能看完,今天先做一半的记录,明天早上继续。
WHAT IS RECURSION?
Algorithmically: a way to design solutions to problems by divide-and-conquer or decrease-and-conquer
- reduce a problem to simpler versions of the same problem
Semantically: a programming technique where a function calls itself
- in programming, goal is to NOT have infinite recursion
- must have 1 or more base cases that are easy to solve
- must solve the same problem on some other input with the goal of simplifying the larger problem input
EXAMPLE OF RECURSION
The algorithm of resusion is divided into two ways: 1.recursiv step: think how to reduce problem to a simpler/smaller version of same problem 2.base case: keep reducing problem until reach a simple case that can be solved directly.
Multiplication
Iterative Solution
“multiply a * b” is equivalent to “add a to itself b itmes”
def mult_iter(a, b):
result = 0
while b > 0;
result += a
b -= 1
return result
Recursion Solution
def mult_recu(a, b):
if b == 1:
return a
else:
return a + mult_recu(a, b-1)
Tower of Hanoi
def printMove(fr, to):
print('move form ' + str(fr) + ' to ' + str(to))
def Towers(n, fr, to ,space):
if n == 1:
printMove(fr, to)
else:
Towers(n-1, fr, space, to)
Towers(1, fr, to, space)
Towers(n-1, space, to, fr)
Palindrome
def isPalindrome(s):
def toChars(s):
s = s.lower()
ans = ''
for c in s:
if c in 'abcdefghijklmnopqrstuvwxyz':
ans += c
return ans
def isPal(s):
if len(s) <= 1:
return true
else:
return s[0] == s[-1] and isPal(s[1:-1])
return isPal(toChars(s))
Fibonacci
def fib(x):
if x == 0 or x == 1:
return 1
else:
# fib(x-1) is the sum of the already existed rabbits in the last month
# fib(x-2) is the sum of the new born rabbits in this month
return fib(x-1) + fib(x-2)
this code has two base cases and calls itself twice, the code is inefficient
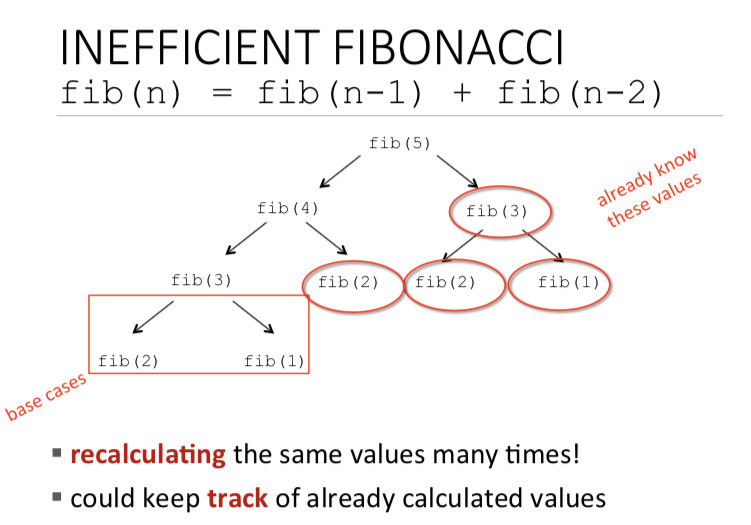
we can improve it by dictionary
def fib_dic(x, d):
if x in d:
return d[x]
else:
ans = fib_dic(x-1, d) + fib_dic(x-2, d)
d[x] = ans
return ans
d = {1:1, 2:2}
print(fib_dic(6, d))
EFFICIENCY GAINS
- Calling fib(34) results in 11,405,773 recursive calls to the procedure
- Calling fib_efficient(34) results in 65 recursive calls to the procedure
- Using dicSonaries to capture intermediate results can be very efficient
-
But note that this only works for procedures without side effects (i.e., the procedure will always produce the same result for a specific argument independent of any other computaSons between calls)