本文记录几种常见的排序算法,代码参考《算法(第4版)》官网
通用代码
// exchange a[i] and a[j]
public static void exch(Comparable[] a, int i, int j) {
Comparable swap = a[i];
a[i] = a[j];
a[j] = swap;
}
// is v < w? public static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
选择排序
现象:
- 设已排序的和未排序的交界处为↑,则每次循环,↑从左往右移动一个位置
- ↑左边的元素(包括↑)固定了,且升序
- ↑ 右边的任一元素全部比左边的所有元素都大
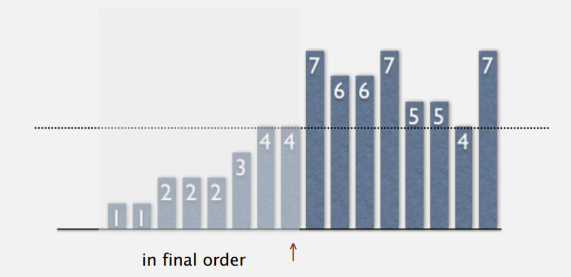
思路:
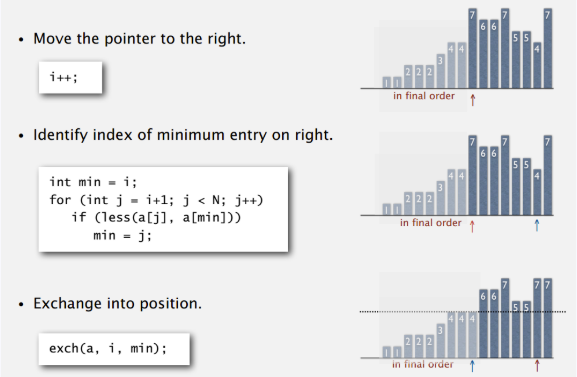
代码:
public static void selectionSort(Comparable[] a) {
if(a == null || a.length < 2) {
return;
}
for(int i = 0; i<a.length; i++) {
int min = i;
for(int j=i+1; j<a.length; j++) {
if(less(a[j], a[min])) {
min = j;
}
}
exec(a, i, min);
}
}
复杂度与特点分析:
- 时间复杂度:O(n^2), 空间复杂度:O(1)
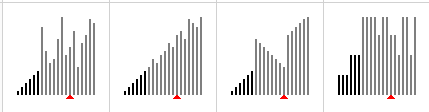
- 运行时间与输入数据的排列状态无关,运行次数都是一样的
- 数据移动最少,交换的次数与数组的大小是线性关系。
冒泡排序
思路:
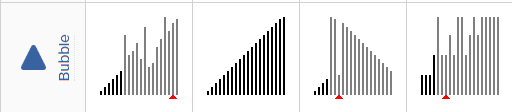
- 从左到右不断交换相邻逆序的元素,在一轮的循环之后,可以让未排序的最大元素上浮到右侧。
- 在一轮循环中,如果没有发生交换,就说明数组已经是有序的,此时可以直接退出。
代码:
public static void bubbleSort(Comparable[] a) {
if (a == null || a.length < 2) {
return;
}
int n = a.length;
boolean isSort = false;
for (int i = n; i > 1 && !isSort; i--) {
isSort = true;
for (int j = 0; j < i - 1; j++) {
if (less(a[j + 1], a[j])) {
exec(a, j + 1, j);
isSort = false;
}
}
}
}
复杂度与特点分析:
- 时间复杂度:O(n^2), 空间复杂度:O(1)
- 运行时间与输入数据的排列状态有关,即在一轮循环中,如果没有发生交换,就说明数组已经是有序的,此时可以直接退出。
插入排序
现象:
- 设已排序的和未排序的交界处为↑,则每次循环,↑从左往右移动一个位置
- ↑左边的元素(包括↑)且升序,但位置不固定(因为后续可能会因插入而移动)
- ↑右边的元素还不可见
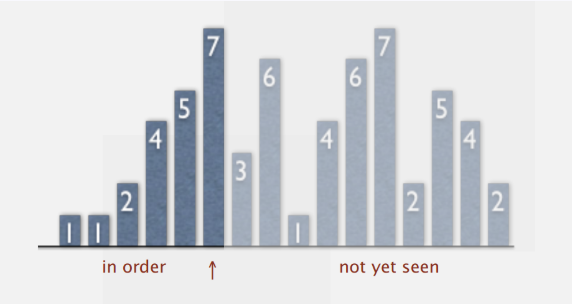
步骤:

代码:
public static void insertSort(Comparable[] a) {
if (a == null || a.length < 2) {
return;
}
int n = a.length;
for (int i = 1; i < n; i++) {
for (int j = i - 1; j >= 0 && less(a[j + 1], a[j]); j--) {
exec(a, j + 1, j);
}
}
}
复杂度与特点分析:
- 时间复杂度:O(n^2)(最坏情况), 空间复杂度:O(1)
- 平均情况下插入排序需要 ~N2/4 比较以及 ~N2/4 次交换;
- 最坏的情况下需要 ~N2/2 比较以及 ~N2/2 次交换,最坏的情况是数组是倒序的;
- 最好的情况下需要N-1次比较和0次交换,最好的情况就是数组已经有序了。
- 运行时间和输入有关,当输入已排序时,时间复杂度是O(n),交换的次数等于输入中倒置(inversion)的个数
- 插入排序适合部分有序数组,也适合小规模数组。
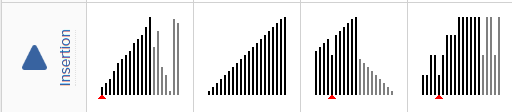
插入排序
对于大规模的数组,插入排序很慢,因为它只能交换相邻的元素,每次只能将逆序数量减少 1。 希尔排序的出现就是为了解决插入排序的这种局限性,它通过交换不相邻的元素,每次可以将逆序数量减少大于 1。 希尔排序使用插入排序对间隔 h 的序列进行排序。通过不断减小 h,最后令 h=1,就可以使得整个数组是有序的。
性质:
- 递增数列一般采用3x+1:1,4,13,40,121,364…..,使用这种递增数列的希尔排序所需的比较次数不会超过N的若干倍乘以递增数列的长度。
- 最坏情况下,使用3x+1递增数列的希尔排序的比较次数是O(N^(3/2))
代码:
public static void shellSort(Comparable[] a) {
if (a == null || a.length < 2) {
return;
}
int n = a.length;
// 3x+1 increment sequence: 1, 4, 13, 40, 121, 364, 1093...
int h = 1;
while (h < n / 3) {
h = 3 * h + 1;
}
while (h >= 1) {
// h-sort the array
for (int i = h; i < n; i++) {
for (int j = i; j >= h && less(a[j], a[j - h]); j -= h) {
exec(a, j - h, j);
}
}
h /= 3;
}
}
基本算法复杂度总结:
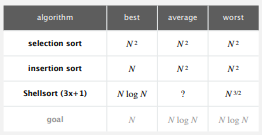
归并排序
思路:
- Divide array into two halves.
- Recursively sort each half.
- Merge two halves.
归并方法的实现: 1.先将所有元素复制到aux[]中,再归并回a[]中。 2.归并时的四个判断:
- 左半边用尽(取右半边元素)
- 右半边用尽(取左半边元素)
- 右半边的当前元素小于左半边的当前元素(取右半边的元素)
- 右半边的当前元素大于/等于左半边的当前元素(取左半边的元素)
// merging
public static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
// copy to aux[]
for (int k = lo; k <= hi; k++) {
aux[k] = a[k];
}
/*
* 1 3 5 7 2 4 6 8
* i j
*/
int i = lo;
int j = mid + 1;
// merge back to a[]
for (int k = lo; k <= hi; k++) {
// 左边元素用尽
if (i > mid) {
a[k] = aux[j++];
// 右边元素用尽
} else if (j > hi) {
a[k] = aux[i++];
// 左边元素比右边小,先进行这一步,保证稳定性
} else if (less(aux[i], aux[j])) {
a[k] = aux[i++];
// 右边元素比左边小
} else {
a[k] = aux[j++];
}
}
}
Top-down mergesort(自顶向下的归并排序)
将一个大数组分成两个小数组去求解。 因为每次都将问题对半分成两个子问题,而这种对半分的算法复杂度一般为O(NlogN),因此该归并排序方法的时间复杂度也为 O(NlogN)。
public static void mergeSort(Comparable[] a, Comparable[] aux, int lo, int hi) {
// base case
if (hi <= lo) {
return;
}
int mid = lo + (hi - lo) / 2;
mergeSort(a, aux, lo, mid);
mergeSort(a, aux, mid + 1, hi);
merge(a, aux, lo, mid, hi);
}
轨迹图:
 由图可知,原地归并排序的大致趋势是,先局部排序,再扩大规模;先左边排序,再右边排序;每次都是左边一半局部排完且merge了,右边一半才开始从最局部的地方开始排序。
由图可知,原地归并排序的大致趋势是,先局部排序,再扩大规模;先左边排序,再右边排序;每次都是左边一半局部排完且merge了,右边一半才开始从最局部的地方开始排序。
改进:
- 对小规模子数组使用插入排序
- 测试数组是否已经有序(左边最大<右边最小时,直接返回)
- 不将元素复制到辅助数组(节省时间而非空间)
Bottom-up mergesort(自底向上的归并排序)
思路:
- 先归并微型数组,从两两归并开始(每个元素理解为大小为1的数组)
- 重复上述步骤,逐步扩大归并的规模,2,4,8….
代码:
// merge sort (bottom up)
public static void mergeSort(Comparable[] a) {
int n = a.length;
Comparable[] aux = new Comparable[a.length];
for (int sz = 1; sz < n; sz = sz + sz) {
for (int lo = 0; lo < n - sz; lo += sz + sz) {
merge(a, aux, lo, lo + sz - 1, Math.min(lo + sz + sz - 1, n - 1));
}
}
}

快速排序
思路: 快速排序通过一个切分元素将数组分为两个子数组,左子数组小于等于切分元素,右子数组大于等于切分元素,将这两个子数组排序也就将整个数组排序了。
下面代码使用随机快排,即每次在数组中随机选择一个数,并与数组最后一个数交换。
public static void quickSort(int[] a) {
if(a == null || a.length < 2 ) {
return;
}
quickSort(a, 0, a.length-1);
}
public static void quickSort(int[] a, int lo, int hi) {
if (lo < hi) {
swap(a, (int) (Math.random() * (hi - lo + 1)) + lo, hi);
int[] position = partition(a, lo, hi);
quickSort(a, lo, position[0] - 1); quickSort(a, position[1] + 1, hi);
}
}
public static int[] partition(int[] a, int lo, int hi) {
int p1 = lo -1;
int p2 = hi;
while(lo < p2) {
if(a[lo] < a[hi]) {
swap(a, ++p1, lo++);
} else if (a[lo] > a[hi]) {
swap(a, --p2, lo);
} else {
lo++;
}
}
swap(a, p2, hi);
return new int[] {p1 +1, p2};
}
public static void swap(int[] a, int i, int j) {
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
性能分析: 快速排序是原地排序,不需要辅助数组,但是递归调用需要辅助栈。
快速排序最好的情况下是每次都正好能将数组对半分,这样递归调用次数才是最少的。这种情况下比较次数为 CN=2CN/2+N,复杂度为 O(NlogN)。
最坏的情况下,第一次从最小的元素切分,第二次从第二小的元素切分,如此这般。因此最坏的情况下需要比较 N2/2。为了防止数组最开始就是有序的,在进行快速排序时需要随机打乱数组。
随机快排的空间复杂度为O(logN)
堆排序
前言:
1.堆结构其实是完全二叉树结构,一个数组结构可以对应成一个完全二叉树结构,如数组[5, 3, 4, 6, 7, 9, 0, 6]可以反映为以下
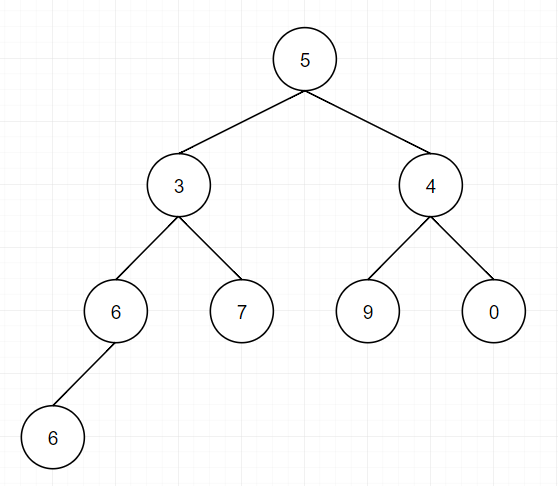
a[i]的左孩子下标为2i+1
a[i]的右孩子下标为2i+2
a[i]的父节点下标为(i-1)/2
2.大根堆:任意一颗子树包括自身,其最大值在头部,例如:
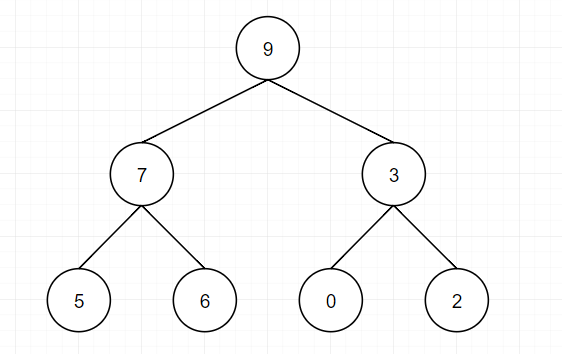
思路: 1.构建堆: 第一可以选择从左到右遍历数组并且进行heapinsert操作,这种方法的复杂度为O(0+log1+log2+log3+…) -> O(N) 第二种可以从右至左进行下沉操作,如果一个节点的两个节点都已经是堆有序,那么进行下沉操作可以使得这个节点为根节点的堆有序。叶子节点不需要进行下沉操作,可以忽略叶子节点的元素,因此只需要遍历一半的元素即可。
2.交换对顶元素与最后一个元素,交换之后对剩下的元素进行heapify操作,每一个元素的复杂度为logN, 一共复杂度为NlogN
代码实现:
public class HeapSort {
public static void heapSort(int[] a) {
if(a == null || a.length<2) {
return;
}
// 构建堆
int size = a.length;
for(int i=0; i<size; i++) {
heapInsert(a, i);
}
swap(a, 0, --size);
while (size > 0) {
heapify(a, 0, size);
swap(a, 0, --size);
}
}
public static void heapInsert(int[] a, int index) {
while (a[index] > a[(index - 1) / 2]) {
swap(a, index, (index - 1) / 2);
index = (index - 1) / 2;
}
}
public static void heapify(int[] a, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
// 一定要判断右孩子是否存在
int max = left + 1 < size && a[left + 1] > a[left] ? left + 1 : left;
max = a[max] > a[index] ? max : index;
if (max == index) {
break;
}
swap(a, max, index);
// 一定要做这一步
index = max;
left = index * 2 + 1;
}
}
public static void swap(int[] a, int i, int j) {
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
}
堆结构其实就是优先级队列结构 性能分析: 1.一个堆的高度为logN,因此在堆中插入元素和删除最大元素的复杂度都为logN。 2.对于堆排序,由于要对N个节点进行下沉操作,因此复杂度为 NlogN。 3.堆排序时一种原地排序,没有利用额外的空间。 4.现代操作系统很少使用堆排序,因为它无法利用局部性原理进行缓存,也就是数组元素很少和相邻的元素进行比较。
排序算法的稳定性及其汇总
首先解释什么叫做算法的稳定性,举例说明: 初始数组:1, 3, 2, 3, 5, 3
可以观察到数组中有三个相同的3,如果算法稳定那排序过后这三个3的相对顺序不会发生改变,他们的顺序还是第一个3, 第二个3, 第三个3.
简单的应用场景举例: 现在有一个表格:
| 水果 | 价格 | 数量 |
|---|---|---|
| 香蕉 | $5 | 2 |
| 苹果 | $2 | 2 |
| 草莓 | $3 | 2 |
现在要求表格按照价格进行排序,然后再按照数量排序,如果算法具有稳定性,那最后的结果是保留了价格的次序,即价格和数量都是排好序的,因为数量排序的时候相同的2其相对位置不变,这样就满足了现实的需求。
冒泡排序:可以做到稳定性,再两个相同的数比较时让右边的数冒泡。
选择排序:不能做到稳定性,
举例: 6 3 3 3 3 1 2 5
当第一个3和2交换的时候,第一个3变成了最后一个3,所以无法实现。
插入排序:可以做到稳定性,当右边的数和左边的数相同时,不让右边的数和左边的交换即可。
归并排序:可以做到稳定性,当左区的数和右区的数相同时让左区的数归并,左区指针往后移一位。
快速排序:不能做到稳定性,如[6, 6, 6, 3, 5],以5为标准进去切分,则切分时第一个6于3交换,不能满足稳定性。
引申的例子:给定一个数组,满足
1.将奇数放左边,偶数放右边。
2.并且保持他们原来的顺序
3.使用inplace的方法,时间复杂度为O(N)
结论,不能满足上述要求,因为经典快排再切分的时候不能满足稳定性,快排与上述例子都满足0-1标准,所以快排做不到,上述例子也做不到。
要想快排实现稳定性,可以参考论文:
STABLE MINIMUM SPACE PARTITIONING IN LINEAR TIME
堆排序:不能满足稳定性
总结: |算法|稳定性|时间复杂度|空间复杂度|备注| |:–:|:—-:|:——–:|:——–:|:–:| |选择排序|x | O(N^2) | 1 | | |冒泡排序|o | O(N^2) | 1 | | |插入排序|o | O(N ~ N^2) | 1 | 时间复杂度和初始顺序有关 | |快速排序|x | O(NlogN) | logN | | |归并排序|o | O(NlogN) | N | | |堆排序|x | O(NlogN) | 1 | |